Page 69 - rohana_journal_No_12-2020-final

Research Journal of the University of Ruhuna, Sri Lanka- Rohana 12, 2020

testing approach is mainly based on the crucial assumption that all the variables are
integrated in order zero, I(0) or order, I(1).

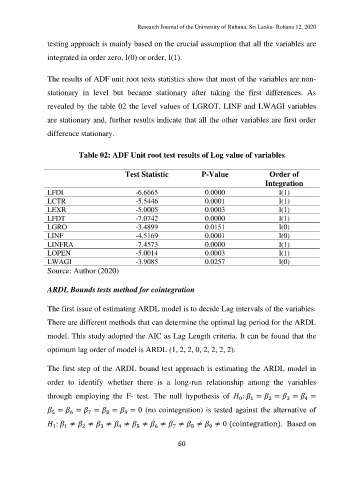
The results of ADF unit root tests statistics show that most of the variables are non-

stationary in level but became stationary after taking the first differences. As
revealed by the table 02 the level values of LGROT, LINF and LWAGI variables

are stationary and, further results indicate that all the other variables are first order
difference stationary.

Table 02: ADF Unit root test results of Log value of variables

Test Statistic P-Value Order of
Integration
LFDI -6.6665 0.0000 I(1)
LCTR -5.5446 0.0001 I(1)
LEXR -5.0005 0.0003 I(1)
LFDT -7.0742 0.0000 I(1)
LGRO -3.4899 0.0151 I(0)
LINF -4.5169 0.0001 I(0)
LINFRA -7.4573 0.0000 I(1)
LOPEN -5.0014 0.0003 I(1)
LWAGI -3.9085 0.0257 I(0)
Source: Author (2020)

ARDL Bounds tests method for cointegration

The first issue of estimating ARDL model is to decide Lag intervals of the variables.
There are different methods that can determine the optimal lag period for the ARDL

model. This study adopted the AIC as Lag Length criteria. It can be found that the

optimum lag order of model is ARDL (1, 2, 2, 0, 2, 2, 2, 2).

The first step of the ARDL bound test approach is estimating the ARDL model in

order to identify whether there is a long-run relationship among the variables
through employing the F- test. The null hypothesis of : = = = =
1
0
2
4
3
= = = = = 0 (no cointegration) is tested against the alternative of
8
9
6
5
7
: ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ 0 (cointegration). Based on
8
9
7
2
3
1
1
6
5
4
60